\(\renewcommand{\vec}[1]{\mathbf{#1}}\)
\(\newcommand{\vecw}{\vec{w}}\) \(\newcommand{\vecx}{\vec{x}}\) \(\newcommand{\vecu}{\vec{u}}\) \(\newcommand{\veca}{\vec{a}}\) \(\newcommand{\vecb}{\vec{b}}\)
\(\newcommand{\vecwi}{\vecw^{(i)}}\) \(\newcommand{\vecwip}{\vecw^{(i+1)}}\) \(\newcommand{\vecwim}{\vecw^{(i-1)}}\) \(\newcommand{\norm}[1]{\lVert #1 \rVert}\) \(\newcommand{\fhat}{\hat{f}}\)
There are many different types of learning settings:
supervised learning: training data includes desired outputs (labels), i.e., training data \(D = \{(\vecx^{(i)}, y^{(i)}) \mid i = 1 \ldots |D|\}\) where each \(\vecx\) is a training example and each \(y\) is its corresponding label. The model is trained to predict the desired output of an input example. Scenarios: classification and regression. This course is mostly about supervised learning.
unsupervised learning: training data does not include labels, i.e., \(D = \{\vecx^{(i)} \mid i = 1 \ldots |D|\}\). Here we aim to find the inherent structures within the data. Scenarios: clustering and dimensionality reduction.
semi-supervised learning: Part of the training data includes labels, while part of it does not, i.e., \(D = D_1 \cup D_2\) where \(D_1 = \{(\vecx^{(i)}, y^{(i)}) \mid i = 1 \ldots |D_1|\}\) and \(D_2 = \{\vecx^{(i)} \mid i = 1 \ldots |D_2|\}\). We use the unlabeled part \(D_2\) as a supplement to improve the model trained on the labeled data \(D_1\).
partially observed learning: Each training example (input) comes with a label (output), and how to get from the input to the output is not annotated. For example: in machine translation (let’s say from English to Chinese), the input data contains one million (English, Chinese) sentence pairs, but the correspondence between English and Chinese words (called “word alignment”) is not annotated.
self-supervised learning: the training data is unlabeled, such as pure text or image, but we predict part of it given the rest. For example, we can train a language model to predict the next word given previous words; we can predict a pixel given the other pixels in an image. This technique has given rise to powerful applications such as ChatGPT.
reinforcement learning: the training data (in this case, the optimal sequence of actions to perform a task) is not labeled, but you can get rewards from the environment. Think about playing chess: there is no annotation to tell you whether each move is good or bad, but at the end of each game, you get a reward signal of win (+1), lose (-1), or draw (0). The goal is to learn from these (often delayed) reward signals and attribute them to individual actions, so that good actions (which eventually lead to positive rewards) will be preferred.
In supervised learning, the training examples are \(D = \{(\vecx^{(i)}, y^{(i)}) \mid i = 1 \ldots |D|\}\) where each label \(y^{(i)} = f(\vecx^{(i)})\) for some unknown function \(f\) which is the underlying function that generates data \(D\). The job of machine learning is to recover \(f\) from data \(D\), or to find a good approximation \(\fhat\) of \(f\) so that \(f(\vecx)\) and \(\fhat(\vecx)\) are close. This function \(\fhat\) is also known as the prediction rule learned from data.
We differentiate two types of function \(f\) which correspond to two subsettings of supervised learning, classification and regression:
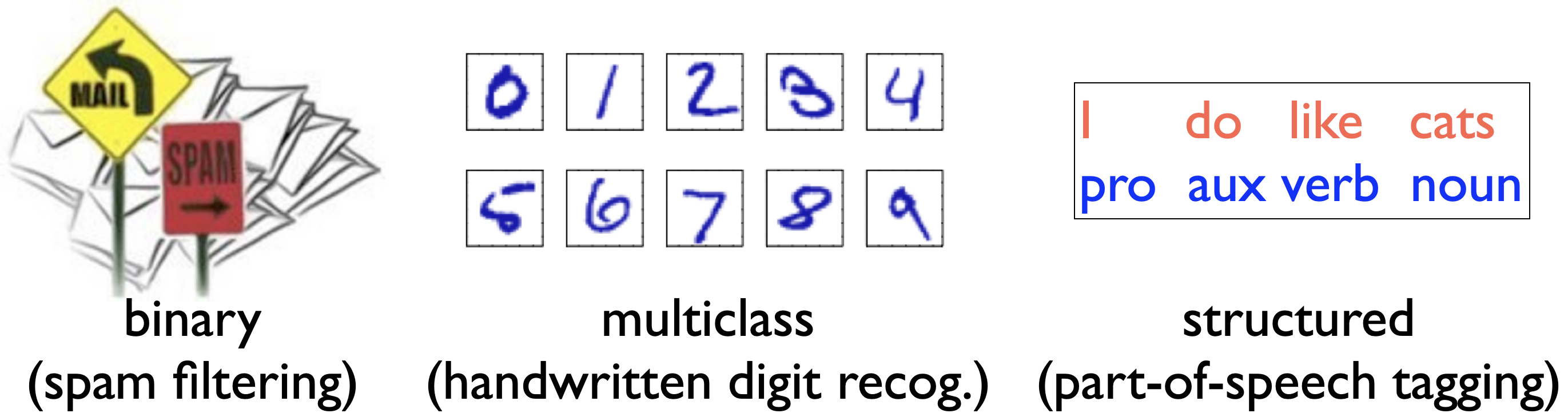
The output \(f(\vecx)\) is discrete, e.g., each \(f(\vecx) \in \{+1,-1\}\) or \(f(\vecx) \in \{0, 1, 2, \ldots, 9\}\). This is known as classification, which is the most widely used setting in machine learning, and also the focus on this course. There are three subtypes of classification:

Supervised learning is particularly useful in the following scenarios:
When there is no human expert
e.g., protein folding, predicting properties of a new molecule
When humans can perform the task but can’t describe it
e.g., face recognition, optical character recognition (OCR), speech recognition
When the desired function changes frequently
e.g., housing price prediction, stock price prediction, spam filtering
When each user needs a customized function
e.g., speech recognition, speech synthesis, spam filtering